Mesin Turing

Mesin Turing adalah perangkat penerima yang menerima bahasa (kumpulan yang dapat dihitung secara rekursif) yang dihasilkan oleh tata bahasa tipe 0. Mesin ini ditemukan pada tahun 1936 oleh Alan Turing. Mesin Turing adalah model matematika yang terdiri dari pita panjang tak terbatas yang dibagi menjadi sel-sel tempat input diberikan.
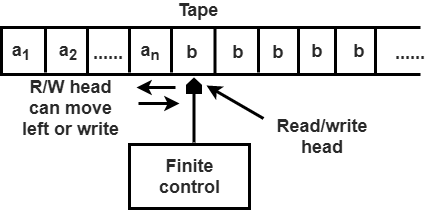
Mesin Turing terdiri dari pita (tape) dengan panjang tak terbatas tempat operasi baca dan tulis dapat dilakukan. Pita itu terdiri dari sel tak terbatas di mana setiap sel berisi simbol masukan atau simbol khusus yang disebut kosong. Ini juga terdiri dari penunjuk kepala yang menunjuk ke sel yang saat ini sedang dibaca dan dapat bergerak di kedua arah.
- Q adalah himpunan keadaan yang terbatas.
- T adalah tape alphabet (simbol yang dapat ditulis pada tape).
- B adalah simbol kosong (setiap sel diisi dengan B kecuali alfabet masukan pada awalnya).
- Σ adalah alfabet masukan (simbol yang merupakan bagian dari alfabet masukan).
- δ adalah fungsi transisi yang memetakan Q × T → Q × T × {L, R}. Bergantung pada status saat ini dan alfabet pita saat ini (ditunjukkan oleh penunjuk kepala), ia akan berpindah ke status baru, mengubah simbol pita (mungkin atau mungkin tidak) dan memindahkan penunjuk kepala ke kiri atau kanan.
- q0 adalah status awal.
- F dalah himpunan keadaan akhir. Jika ada status F tercapai, string input diterima.
Contoh Mesin Turing
Agar lebih paham dengan Mesin Turing, berikut adalah contohnya.
Buatlah Mesin Turing untuk L = {0n1n | n ≥ 1}
- Q = {q0, q1, q2, q3}, di mana q1 adalah initial state
- T = {0, 1, X, Y, B}, di mana B merepresentasikan simbol kosong
- Σ = {0, 1}
- F = {q3}
Maka fungsi transaksi δ menjadi tabel di bawah ini:
| 0 | 1 | X | Y | B | |
|---|---|---|---|---|---|
| q0 | (q1, X, R) | (q3, Y, R) | |||
| q1 | (q1, 0, R) | (q2, Y, L) | (q1, Y, R) | ||
| q2 | (q2, 0, L) | (q0, X, R) | (q2, Y, L) | ||
| q3 | (q3, Y, R) | Halt |
Mari kita coba bagaimana Mesin Turing bekerja dengan input 0011. Permulaainya dimulai dari 0 yang ditebali berwarna merah.
| B | 0 | 0 | 1 | 1 | B |
Penyelesaian :
- Langkahnya adalah δ (q0, 0) = (q1, X, R). Artinya, ia akan pergi ke status q1, ganti 0
dengan X dan kepala akan bergerak ke kanan sebagai:
B X 0 1 1 B - Perpindahan akan menjadi δ (q1, 0) = (q1, 0, R) yang berarti ia
akan tetap dalam keadaan
yang sama dan tanpa mengubah simbol apapun, ia akan bergerak ke kanan seperti:
B X 0 1 1 B - Perpindahannya menjadi δ (q1, 1) = (q2, Y, L) yang artinya akan
berpindah ke keadaan q2
dan ubah 1 menjadi Y, maka akan berpindah ke kiri seperti:
B X 0 Y 1 B - Perpindahannya menjadi δ (q2, 0) = (q2, 0, L) yang artinya akan
berpindah ke keadaan q2
dan ubah 0 menjadi 0, maka akan berpindah ke kiri seperti:
B X 0 Y 1 B - Perpindahannya menjadi δ (q2, X) = (q0, X, R) yang artinya akan
berpindah ke keadaan q0
dan ubah X menjadi X, maka akan berpindah ke kanan seperti:
B X 0 Y 1 B - Perpindahannya menjadi δ (q0, 0) = (q1, X, R) yang artinya akan
berpindah ke keadaan q1
dan ubah 0 menjadi X, maka akan berpindah ke kanan seperti:
B X X Y 1 B - Perpindahannya menjadi δ (q1, Y) = (q1, Y, R) yang artinya akan
berpindah ke keadaan q1
dan ubah Y menjadi Y, maka akan berpindah ke kanan seperti:
B X X Y 1 B - Perpindahannya menjadi δ (q1, 1) = (q2, Y, L) yang artinya akan
berpindah ke keadaan q2
dan ubah 1 menjadi Y, maka akan berpindah ke kiri seperti:
B X X Y Y B - Perpindahannya menjadi δ (q2, Y) = (q2, Y, L) yang artinya akan
berpindah ke keadaan q2
dan ubah Y menjadi Y, maka akan berpindah ke kiri seperti:
B X X Y Y B - Perpindahannya menjadi δ (q2, X) = (q0, X, R) yang artinya akan
berpindah ke keadaan q0
dan ubah X menjadi X, maka akan berpindah ke kanan seperti:
B X X Y Y B - Perpindahannya menjadi δ (q0, Y) = (q3, Y, R) yang artinya akan
berpindah ke keadaan q3
dan ubah Y menjadi Y, maka akan berpindah ke kanan seperti:
B X X Y Y B - Perpindahannya menjadi δ (q3, Y) = (q3, Y, R) yang artinya akan
berpindah ke keadaan q3
dan ubah Y menjadi Y, maka akan berpindah ke kanan seperti:
B X X Y Y B - Menggunakan gerakan δ (q3, B) = Halt, itu akan berhenti dan diterima.
Seperti itulah contoh dari Mesin Turing. Jika masih belum paham, coba dipahami perlahan-lahan.
Mengapa Mesin Turing Penting?
Turing tidak menemukan mesin. Turing datang dengan model abstrak untuk semua mesin. Dengan kata lain, algoritma apa pun dapat dibuat di Mesin Turing.
Ini adalah deskripsi teoretis tentang komputer. Untuk itulah Turing menggunakan Mesin Turing. Dia memikirkannya sehingga dia bisa membuktikan properti hal-hal yang dapat dihitung secara umum. Sebelumnya, kami tidak benar-benar tahu apa-apa tentang batasan algoritma. Kami tidak tahu persis apa yang bisa dihitung.
Yang keren adalah penemuan luar biasa ini hanyalah produk sampingan dari Turing yang mencoba menjawab beberapa pertanyaan matematika fundamental, tetapi dalam prosesnya dia menciptakan dasar dari semua komputer yang kita gunakan saat ini.
Ini semua terdengar bagus bagi kami yang duduk di sini membaca ini di komputer tujuan umum kami. Namun perlu diingat bahwa Turing menulis ini pada tahun 1936. Ini sebelum komputer yang dapat diprogram. Faktanya, pada saat itu, "komputer" mengacu pada seseorang, bukan mesin. Dan pemikiran pada saat itu adalah bahwa komputer hanya dapat dibuat untuk satu tugas. Tapi Turing percaya sebaliknya. Dia percaya bahwa Anda dapat membuat satu mesin yang dapat diprogram untuk melakukan tugas apa pun. Ternyata itu benar, karena Anda sedang menggunakan salah satunya.
Adanya mesin-mesin dengan sifat ini mempunyai konsekuensi penting bahwa, selain pertimbangan kecepatan, berbagai mesin baru tidak perlu dirancang untuk melakukan berbagai proses komputasi. Semuanya dapat dilakukan dengan satu komputer digital, yang diprogram secara sesuai untuk setiap kasus. - Turing, 1950.
